Pengertian Bilangan, Jenis-Jenisnya Beserta Contohnya

kanggustri.xyz - Artikel kali ini akan membahas tentang pengertian bilangan dan jenis-jenisnya, seperti bilangan cacah, bilangan asli, bilangan bulat, bilangan bulat positif, negatif, bilangan nol, bilangan genap, ganjil, bilangan prima, bilangan pecahan, pecahan desimal, pecahan persen, bilangan rasional, dan bilangan romawi. Serta diberikan beberapa contohnya. Untuk lebih jelasnya silahkan simak ulasannya di bawah ini ya!

Daftar Isi Artikel

• 1 Pengertian Bilangan
• 2 Jenis-Jenis Bilanagan
  • 2.1Bilangan Cacah
  • 2.2Bilangan Asli
  • 2.3Bilangan Bulat
  • 2.4Bilangan Bulat Positif
  • 2.5Bilangan Bulat Negatif
  • 2.6Bilangan Nol
    • 2.6.1Sifat Sifat Bilangan Nol
• 3 Bilangan Genap
• 4Bilangan Ganjil
• 5Bilangan Prima
• 6Bilangan Pecahan
• 7Bilangan Pecahan Desimal
• 8Bilangan Pecahan Persen
• 9Bilangan Romawi
  • 9.1Cara Penulisan Bilangan Romawi
  • 9.2Cara Membaca Bilangan Romawi

Pengertian Bilangan

Bilangan digunakan untuk menyatakan jumlah suatu benda. Bilangan adalah satuan dalam sistem matematika yang abstrak, dapat diunitkan, ditambah, atau dikalikan.

Contoh bilangan:

Lambang Bilangan	1	2	3	4
Dibaca	Satu	Dua	Tiga	Empat

Sekumpulan bilangan biasanya dinyatakan dalam bentuk himpunan bilangan. Penulisan himpunan bilangan digambarkan dengan menggunakan tanda kurung kurawal "{....}".

Contoh:

Tulislah dua buah gambar heart dalam bentuk himpunan!

Penyelesaian:

{❤❤}

Jenis-Jenis Bilangan

Bilangan Cacah

Bilangan cacah adalah bilangan yang dimulai dari angka nol (0).

Contoh:

{0,1,2,3,4,...}

Bilangan Asli

Bilangan asli adalah bilangan yang dimulai dari angka satu (1).

Contoh:

{1,2,3,4,5,...}

Bilangan Bulat

Bilangan bulat terdiri dari bilangan positif, bilangan negatif, dan bilangan nol (0). Jadi, kecuali bilanagan pecahan, semua bilangan termasuk ke dalam bilangan bulat.

Bilangan Bulat Positif

Bilangan bulat positif terdiri dari bilangan asli.

Contoh:

{1,2,3,4,5,...}

Bilangan Nol

Bilangan nol,yaitu (0).

Bilangan Bulat Negatif

Bilangan bulat negatif merupakan bilangan yang nilainya berlawanan dengan bilangan bulat positif.

Contoh:

{-1,-2,-3,...}

Dalam bentuk himpunan, bilangan bulat dapat ditulis:

{...,-3,-2,-1,0,1,2,3,...}

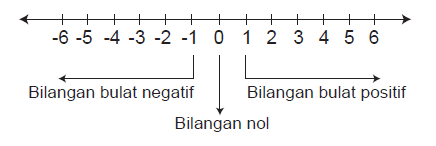
Dalam bentuk garis bilangan , bilnagan ulat dapat di tulis:

Dari garis bilangan bulat di atas didapat:

➣ Letak bilangan negatif pada garis bilangan adalah di sebelah kiri bilangan nol.

➣ Letak bilangan positif pada garis bilangan adalah di sebelah kanan bilangan nol.

➣ Bilangan bulat yang letaknya di sebelah kanan, nilainya lebih besar dibandingkan dengan bilangan bulat yang letaknya di sebelah kiri.

Bilangan Genap

Bilangan genap adalah bilangan yang nilainya habis dibagi dengan bilangan dua.

Contoh:

{0,2,4,6,8,...}

Pembuktian:
0:2=0
2:2=1
4:2=2
6:2=3
8:2=4 dst.

Hasil baginya merupakan bilangan bulat (habis dibagi, tanpa ada nilai desimal).

Bilangan Ganjil

Bilangan ganjil adalah bilangan yang tidak habis di bagi dengan bilangan dua.

Contoh:

{1,3,5,7,...}

Pembuktian:
1:2=0.5
3:2=1.5
5:2=2.5

Hasil baginya bukan merupakan bilangan bulat (tidak habis dibagi, ada nilai desimal).

Bilangan Prima

Bilangan prima adalah bilangan yang hanya mempunyai dua faktor, yaitu bilangan 1 dan bilangan itu sendiri.

Contoh:

{2, 3, 5, 7, 11, 13, 17, 19, ...}

Uraian:

2 ➝ mempunyai faktor 1 dan 2
3 ➝ mempunyai faktor 1 dan 3
5 ➝ mempunyai faktor 1 dan 5

Bilangan Pecahan

Bilangan pecahan adalah bilangan yang terdiri dari bilangan pembilang dan penyebut.

^a/_b

Keterangan:
a = Pembilang
b = Penyebut

Contoh:
{¹/₂, ²\₃, ³\₅, ....}

Bilangan pecahan yang bilangan pembilangdan penyebut sama nilainya adalah satu (1).

Contoh:

⁴\₄ = 1

Bilangan Pecahan Desimal

Bilngan desimal merupaan bentuk lain dari bilangan pecahan.

Contoh:

{1,2; 2,3; 5,4; ...}

Bilangan pecahan desimal didapat dengan cara membagi bilangan penyebut dengan bilangan pembilang pada bilangan pecahan biasa.

Contoh:

¹/₂ = 1:2 = 0,5

Bilangan Pecahan Persen (%)

Persen mempunyai arti per seratus. Jadi, bilangan pecahan persen artinya bilangan pecahan tersebut mempunyai bilangan penyebut seratus (100).

Contoh:

20% = ²⁰/₁₀₀

Sifat-Sifat Bilangan Nol

1. Jika berdiri sendiri, bilangan nol tidak mempunyai nilai.

2. Jika dijumlahkan dengan bilngan berapapun, hasil penjumlahannya sama dengan nilai bilangan penjumlahnya.

Contoh:

0 + 2 = 2

18 + 0 = 18

3. Bilangan berapapun jika dikurangi dengan bilangan nol, hasil pengurangannya sama dengan nilai bilangan itu sendiri.

Contoh:

1 - 0 = 1

9 - 0 = 9

4. Bilangan berapapun jika dikali dengan bilangan nol, hasil perkaliannya adalah nol. 

Contoh:

5 X 0 = 0

20 X 0 = 0

5. Bilngan berapapun jika dibagi dengan bilangan nol, hasil pembagiannya adalah tak terhingga. 

Contoh:

1 : 0 = ~ (tak terhingga)

9 : 0 = ~

6. Bilangan no tidak mempunyai nilai positif (+) dan nilai negatif (-).

Bilangan Romawi

Bentuk dasar bilangan romawi.

Bilangan Cacah	Bilangan Romawi
1	I
2	II
3	III
4	IV
5	V
6	VI
7	VII
8	VIII
9	IX
10	X
50	L
100	C
500	D
1000	M

 Cara Penulisan Bilangan Romawi

1. Penulisan bilangan romawi didasarkan pada sistem pengulangan, penjumlahan, dan pengurangn.

2. Sistem pengulngan pada bilangan romawi dapt dilakukan sebanyak-banyaknya adalah tiga kali pengulangan.

Contoh:

a. Penulisan bilanagan romawi berdasarkan sistem pengulangan:

20 = XX

30 = XXX

b. Penulisan bilangan romawi berdasarkan sistem penjumlahan:

7 = VII

13 = XIIIX

c. Penulisan bilangan romawi berdasarkan sistem pengurangan:

4 = IV

9 = IX

Cara Membaca Bilangan Romawi

➣ Secara umum, bilangan romawi dibaca dari arah kiri ke kanan.

➣ Bentuk bilangan romwi yang diikuti oleh bilangan romawi yang nilinya sama atau lebih kecil, nilai bilangan romawi yang mengikutinya harus ditambahkan ke nilai bilangan romawi yang diikuti.

Contoh:

XXXI = 31

Penjelasan:

➤ Bilangan romawi X dan X mempunyai nilai yang sama. Jadi, kedua bilangan romawi tersebut dijumlahkan: X + X + X = 10 +10 + 10 = 30.

➤ Bilangan romawi I (1) mempunyai nilai lebih kecil daripada XXX (30). Jadi, bilangan romawi I dijumlahkan ke bilangan romawi XXX.

➤ Hasilnya: X + X + X + I = 10 + 10 + 10 + 1 = 31.

➣ Bentuk bilangan romawi yang diikuti oleh bilangan romawi yang nilainya lebih besar, nilai bilangan yang mengikutinya harus dikurangi dengan nilai angka bilangan romawi yang diikuti.

Contoh:
IV = 4

Penjelasan:
➤ Bilangan romawi I (1) mempunyai nilai yang lebih kecil daripada nilai bilangan romawi V (5). Jadi, bilangan romawi V (5) harus dikurangi bilangan romawi I (1).
➤ Hasilnya: IV = V -I = 5 -1 =4.

Demikiannlah pengertian bilangan, jenis-jenisnya beserta contohnya. Semoga dapat membantu kamu semua dalam pengerjaan tugas-tugas kamu semua.  Nantikan artikel menarik lainnya dan mohon kesediaannya untuk menshare keteman-teman kamu supaya mendapatkan ilmunya juga.

Materi Terkait:

• Bilangan
• Bilangan Cacah
• Bilangan Asli

Share this post